Радикальное продление жизни – часть 12. Часы долголетия

Как оценить эффективность методов продления жизни

Внешние изменения, либо улучшение каких-то показателей здоровья не гарантируют влияние на само старение и продолжительность жизни.

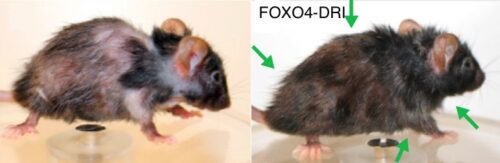
На рисунке одна и та же мышь до и после терапии с помощью FOXO4-DRI [pubmed.ncbi.nlm.nih.gov/28340339].

Исследователи утверждают, что после терапии с помощью FOXO4-DRI мыши омолодились. Как они это определили? На глаз? Непонятно, было ли омоложение, либо мыши просто стали выглядеть лучше.

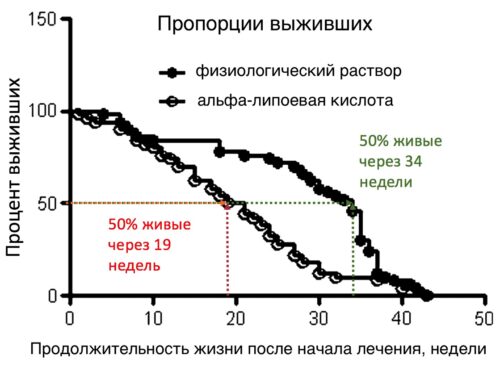В другом исследовании терапия альфа-липоевой кислотой, хотя и улучшала память и снижала количество ошибок в когнитивных тестах, но сокращала продолжительность жизни мышей. 

На рисунке мыши, получавшие альфа-липоевую кислоту, имели медиану выживаемости 20 недель после начала лечения по сравнению с контрольными мышами, у которых медиана выживаемости составляла 34 недели [ncbi.nlm.nih.gov/pubmed/22785389].

Итак, как так получается, что мыши демонстрировали некоторые признаки более молодого возраста, но жили меньше? Было ли здесь омоложение? Как это понять?

«Если вы не умеете это измерять, то вы не знаете, о чем вы говорите», - приблизительно так говорил Лорд Келвин, ученый, который применял законы физики и математики к любым научным и техническим проблемам (примечание, это интерпретация его высказывания по смыслу). Давайте попробуем измерить старение. 

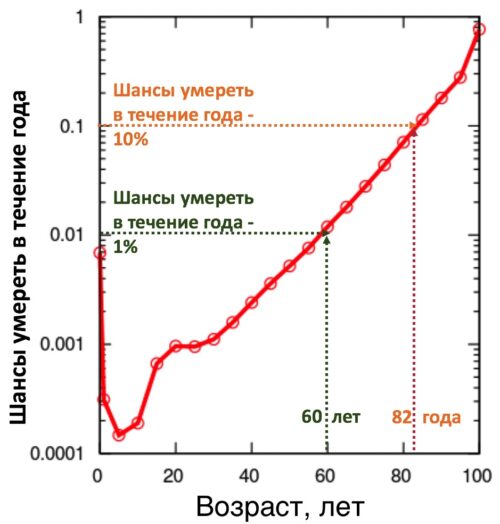Математически старение — это процесс, приводящий к росту шансов умереть в каждом следующем возрасте. Не к повышению шансов умереть с возрастом, так как у нестареющих животных также растут шансы умереть с возрастом, а именно "росту шансов умереть в каждом следующем возрасте".

На рисунке - кривая Гомпертца-Мейкхама. Оценка шансов смерти человека в каждом возрасте для США в 2003 году. В возрасте 60 лет риск не дожить до 61 года всего 1%. Тогда как в 82 года риск не дожить до 83 лет уже 10%. Вот, что значит "рост шансов умереть в каждом следующем возрасте". Это важно не путать. При "нестарении" шансы умереть есть все равно, но в 61 год и в 82 года риск не дожить до следующего года при "нестарении" будут одинаковыми. 

• cdc.gov/nchs/data/nvsr/nvsr54/nvsr54_14.pdf
• pubmed.ncbi.nlm.nih.gov/25750242
• pubmed.ncbi.nlm.nih.gov/9074828

Старение на уровне популяции пытались измерять Бенджамин Гомпертц - английский математик, статистик, а также Валодди Вейбулл. В этой статье будем использовать оценку старения, которую создал Бенджамин Гомпертц. 

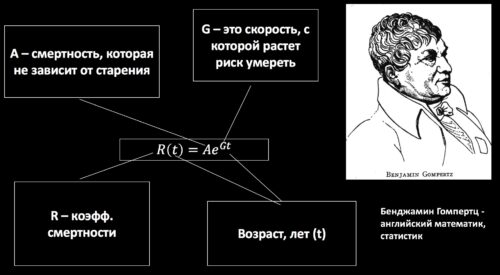На рисунке уравнение Гомпертца. R (t) - это риск умереть в возрасте t. Если нужно узнать риск умереть в течение года в возрасте 60 лет, то t =60. Если риск умереть в возрасте t = 1%, значит из 100 человек в возрасте 60 лет один человек, наиболее вероятно, не доживет до 61 года. То есть, 1% из наблюдаемой совокупности. A - это риск смертности, который не зависит от скорости старения, то есть его можно снизить в любом возрасте. Например, стоит прекратить курить, и риск умереть (A) снизится без влияния на скорость старения (G). G -это скорость старения. Учитывая то, что молодые тоже умирают и тоже от болезней, риск смерти (А), который не зависит от старения, всегда есть даже у нестареющих животных. Скорость, с которой растет риск умереть в каждом возрасте t, - это и есть скорость старения (G). e - это число равное приблизительно 2,71828. 

У метода Гомпертца есть свои ограничения, как и у любой другой метрики. Но о них мы поговорим немного позже. 

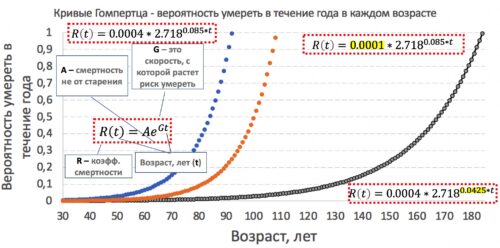Используя закон Гомпертца, построим кривые смертности (см. рисунок). Синяя кривая смертности имеет в уравнении смертность (А), равную 0.0004, которая не зависит от скорости старения. Оранжевая кривая смертности, это смертность с аналогичной скоростью старения (G), но с другой (А), равной 0.0001. То есть, смертность сократилась в 4 раза с 0.0004 до 0.0001. Обратим внимание, что оранжевая кривая смертности сдвинута относительно синей ПАРАЛЛЕЛЬНО. В уравнении черной кривой смертности в отличии от оранжевой ничего не изменилось кроме того, что скорость старения (G) сократилась в 2 раза - с 0.085 до 0.0425. Мы видим, что при изменении скорости старения черная кривая смертности не сдвигается параллельно вправо, а меняет УГОЛ НАКЛОНА.

Но сама кривая смертности нам мало о чем говорит, если нет понимания, по каким законам она формируется. Давайте углубляться.

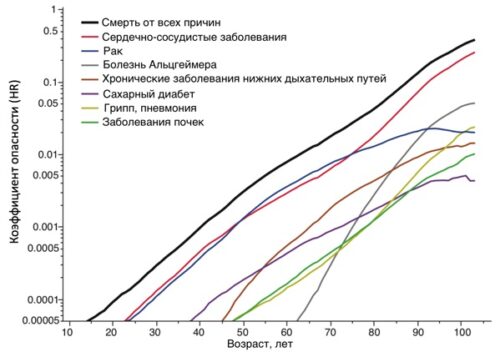
Так кривая общей смертности является суммой всех кривых смертности от каждой причины (от каждого заболевания по международной классификации заболеваний - МКБ). Для наглядности эти заболевания можно сложить в группы. Например, сердечно-сосудистые заболевания, рак и так далее. 

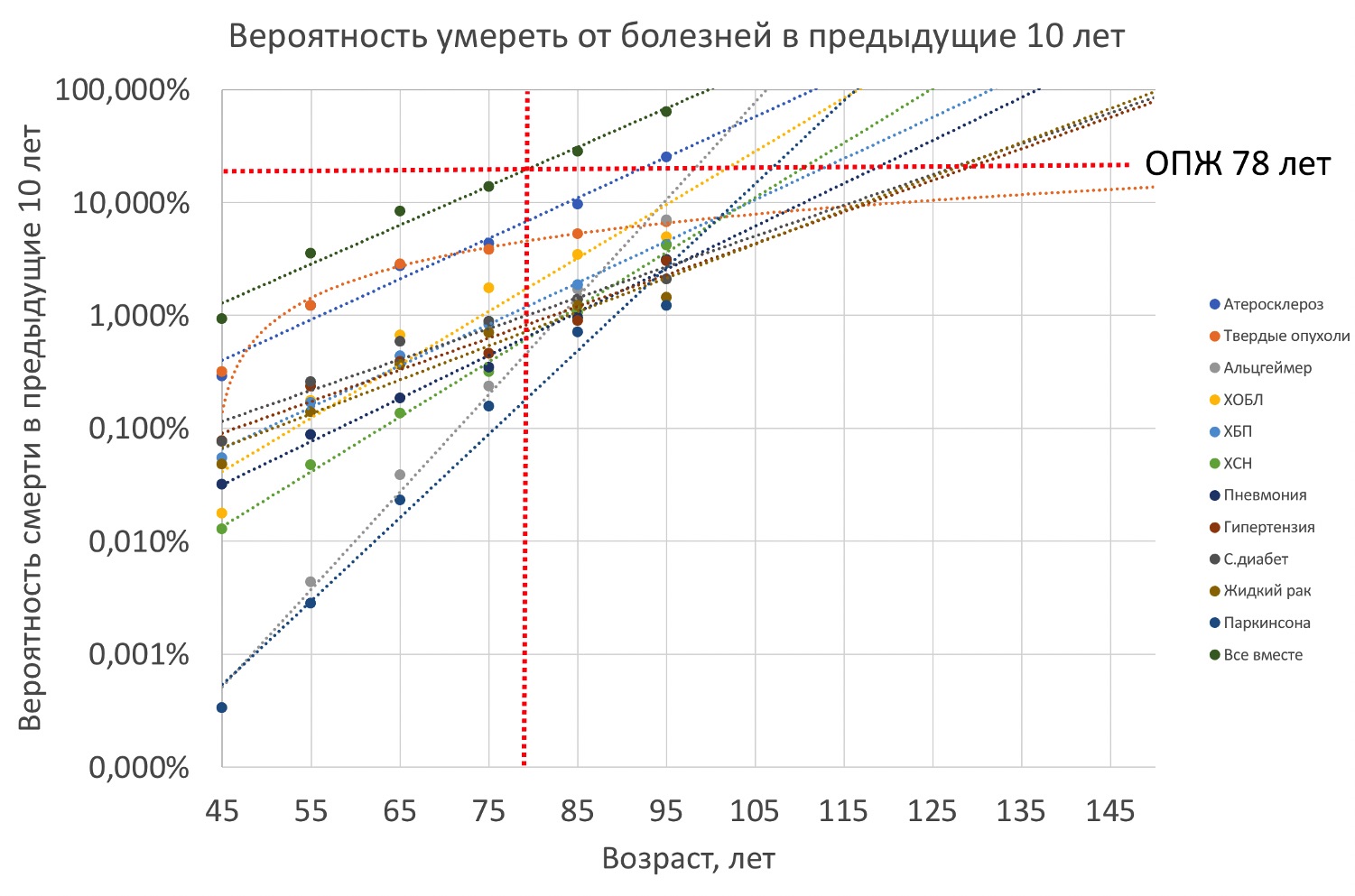
На рисунке показан риск смерти от семи наиболее частых групп причин неслучайной смерти, что соответствует 70% всех смертей, зарегистрированным в США в 2015 г. [pubmed.ncbi.nlm.nih.gov/30099284]. 

Уравнение Гомпертца R(t) = A*e^(G*t), где G -  это скорость старения. Зная скорость старения, можно рассчитать время удвоения смертности, Mortality Rate Doubling Time (MRDT). MRDT = ln(2)/G.

G человека = 0.06931; MRDT = ln(2)/0.06931 = 0.6931/0.06931 = 10 лет. Это означает, что у людей риск умереть удваивается каждые 10 лет. По другим данным - раз в 8 лет.

Также, G = ln(2) / MRDT.

Старение, как математический процесс – это фундаментальная теория, которая применяется с 1975 года до сих пор. Расчет MRDT (Mortality Rate Doubling Time) в 1975 году впервые был предложен американским эпидемиологом Ричардом Дж. Пайнтом. И до сих пор многие авторитетные геронтологи во всем мире используют MRDT и функцию Гомпертца для оценки скорости старения [genetics.org/content/204/3/905], [academic.oup.com/genetics/article/208/4/1617/6084259]. 

У овцы риск умереть удваивается каждые 1,5 года, а у мышей - каждые 3,5 месяца.

Откуда берется смертность, которая не зависит от старения?

Итак, если вы читаете какое-либо исследование, то не верьте в замедление скорости старения, если исследователи его не измеряли с применением закона Гомпертца, либо Вейбулла или других методов, которые в своей основе строятся на математических законах. Эпигенетические часы "будто" старения не доказаны для измерения скорости старения. Об этом бы уже говорили в статье "Радикальное продление жизни – часть 11. Причины провала науки о старении человека". Либо об этом можно прочитать в этом исследовании [pubmed.ncbi.nlm.nih.gov/29718110].

А теперь еще раз вспомним уравнение Гомпертца. Вас ничего в нем не удивляет? Откуда берется смертность, которая не зависит от старения? Разве нестарение не означает бессмертие? 

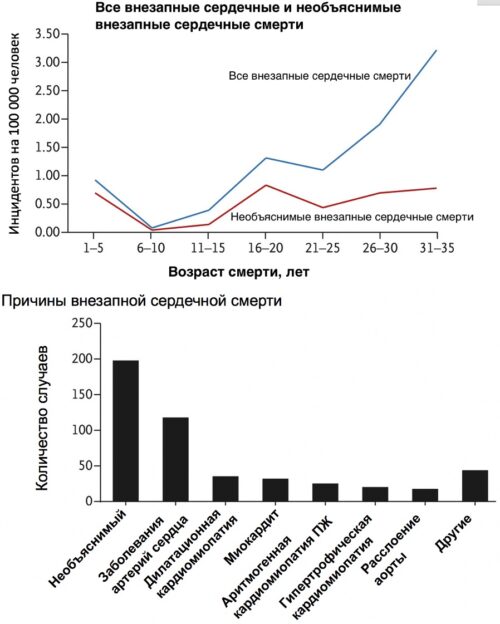
На самом деле молодые тоже умирают от рака, от сердечно-сосудистых заболеваний и так далее. 

На рисунке статистика смертности от сердечно-сосудистых заболеваний среди молодых. Среди них заболевания артерий сердца, дилатационная кардиомиопатия, миокардит, аритмогенная кардимиопатия правого желудочка, гипертрофическая кардимиопатия, расслоение аорты [pubmed.ncbi.nlm.nih.gov/27332903]
[pubmed.ncbi.nlm.nih.gov/31889304]. 

Итак, молодые хоть и редко, но все же умирают от болезней. Поэтому старение не означает бессмертие. Даже в 50 лет, когда мы уже не молоды, можно снизить уровень пагубного влияния на организм, чтобы снизить риск смертности без влияния на скорость старения.

По этой причине люди могут иметь одинаковую скорость старения, но выглядеть моложе или старше.

Это и называется фенотипическим возрастом.

Фенотипитический возраст зависит не только от скорости старения, но и от смертности и заболеваемости, которая не зависит от скорости старения, которая в уравнении Гомпертца R(t) = A*e^(G*t) обозначается, как (A).

Рисунок. Ефремов и Брэд Пит – оба 1963 года рождения. Но выглядят так, будто первый старше второго.

Победа над старением не сделает нас бессмертными

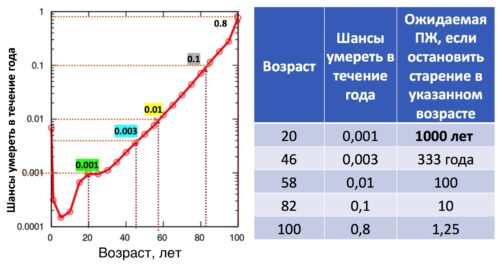Если бы у людей в 20 лет скорость старения стала равна нулю, то сколько бы они в среднем прожили? Какова была бы их ожидаемая продолжительность жизни? Согласно теории вероятности, ожидаемая продолжительность жизни (ОПЖ) = 1 / шансы умереть в течение года. 

Рисунок. Риск умереть в течение года в каждом возрасте. В 20 лет - 0.001, в 46 лет 0.003, в 58 лет 0.01, в 82 года 0.1, в 100 лет 0.8. Ожидаемая продолжительность жизни при нестарении, начиная с 20 лет = 1 / 0.001 = 1000 лет; при нестарении, начиная с 46 лет = 1 / 0.003 = 333 года и так далее.

Но это у людей. Многие животные имеют на столько высокий риск смертности в молодости, что при остановке старения все равно будут жить не долго. Какова ожидаемая продолжительность жизни мухи дрозофилы, если остановить ее старение?

• Для самцов дрозофилы в возрасте 1 недели риск смерти в течение следующей недели составляет 0,0111 (1,11%).
• Прекращение старения для таких дрозофил означает, что их риск не увеличится.
• Давайте подсчитаем продолжительность их жизни.
• Ожидаемая продолжительность жизни = 1/0.0111 = 90 недель жизни (или более 1 года и 8 месяцев)

Таким образом нестареющая муха дрозофила будет иметь ожидаемую продолжительность жизни менее 2-х лет. Это вовсе не бессмертие. 

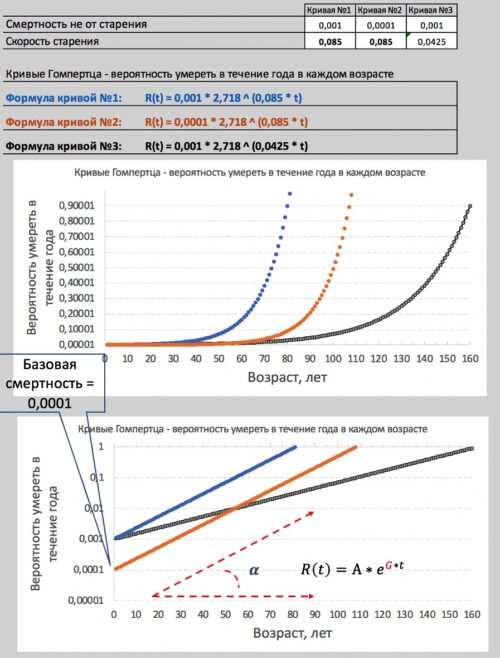Рисунок. Кривые смертности Гомпертца, согласно закону Гомпертца - R(t) = A*e^(G*t). Синяя кривая - исходная, которая имеет уравнение 0,001*2,718^(0,085*t). Оранжевая кривая имеет 10-ти кратное (с 0.001 до 0.0001) снижение смертности (А), которая не зависит от скорости старения (G). Черная кривая смертности по сравнению с синей имеет более низкую скорость старения (G), которая снижена с 0.085 до 0.0425. 

График ниже - тот же самый график, но в логарифмической шкале по вертикали. Из-за логарифмической шкалы кривые смертности превращаются в прямые линии. 

Начало кривых смертности, где находится их самое низкое значение по вертикальной оси - это и есть (А) из уравнения Гомпертца. А скорость старения (G) - это угол наклона кривых смертности.

Таким образом мы видим, что синяя и оранжевая линии имеют одинаковый наклон и, следовательно, одинаковые скорости старения (G), но разные смертности (А), которые не зависят от скорости старения. Так как их скорость старения не изменилась, они параллельны друг другу. Это важно запомнить. 

А черная кривая смертности имеет другую скорость старения (G) в отличии от синей и оранжевой, поэтому угол ее наклона отличается.

В сухом остатке, при графическом изображении кривых смертности изменение угла наклона между двумя кривыми смертности говорит об изменении скорости старения, а параллельный сдвиг говорит об изменении смертности, которая не зависит от скорости старения. Но это утверждение имеет ограничения. 

1. Если вторая кривая смертности имеет более низкое значение (G) при сравнении с первой, а также увеличенную медианную продолжительность жизни и одновременно еще в большей степени увеличенную максимальную продолжительность жизни, то мы можем делать вывод о замедлении скорости старения для второй кривой смертности в сравнении с первой. И наоборот. 
2. Если вторая кривая смертности имеет более низкое значение (G) при сравнении с первой, но не имеет увеличение максимальной и одновременно медианной продолжительности жизни, то мы не может делать выводы об изменении скорости старения для второй кривой смертности в сравнении с первой. И наоборот.

Как выглядит математически старение, нестарение и омоложение при одинаковой смертности, не зависящей от старения?

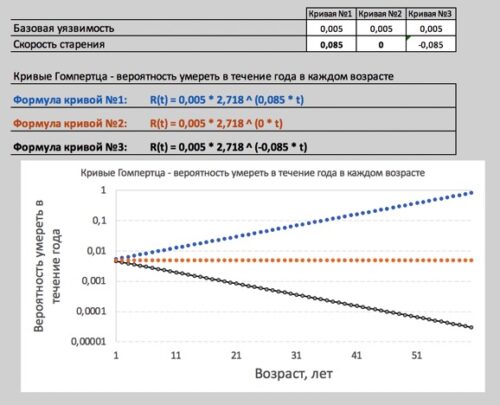На рисунке изображены три кривые смертности в логарифмической шкале. Синяя кривая смертности - исходная, которая имеет уравнение 0,001*2,718^(0,085*t). Синяя кривая - это кривая смертности стареющего организма. Оранжевая кривая смертности, которая имеет уравнение 0,001*2,718^(0*t). Оранжевая кривая - это кривая смертности нестареющего организма. Так как организм не стареет, то и скорость старения (G) в ее уравнении равна 0 соответственно. Черная кривая смертности, которая имеет уравнение 0,001*2,718^(-0,085*t). Черная кривая - это кривая смертности омолаживающегося организма. Так как организм омолаживается, то и скорость старения (G) в ее уравнении имеет знак минус, так как старение идет в обратном направлении  - омоложение. 

Поэтому, когда исследователи говорят об омоложении, то нужно задать вопрос, получили ли они скорость старения со знаком минус при определении скорости старения, либо "омоложение" используется для "красного словца". 

Часы долголетия

Итак, с учетом всего выше рассмотренного, давайте создадим часы долголетия. Как? Прям сегодня? Конечно!
Но тикать будет математика! Есть плохая и одновременно хорошая новость. Уменьшать скорость старения для продления жизни мы пока не умеем. 

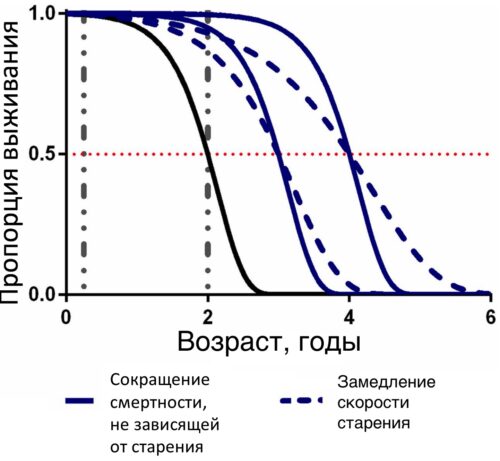
Еще ни в одном эксперименте не удавалось уменьшить скорость старения мышей для продления жизни с помощью изменения в генах [genetics.org/content/204/3/905] [academic.oupф.com/genetics/article/208/4/1617/6084259]. У мышей мутации, продлевающие продолжительность жизни, не уменьшают скорость старения (G), но уменьшают только смертность (А), которая не зависит от старения (G). На рисунке кривые выживания, иллюстрирующие продление жизни за счет уменьшения скорости старения (G) по Гомпертцу R(t) = A*e^(G*t), имеют измененный угол наклона и отображаются пунктирной линией. На рисунке кривые выживания, иллюстрирующие продление жизни за счет уменьшения смертности (А), которая не зависит от старения (G) по Гомпертцу, имеют параллельный сдвиг вправо и отображаются сплошной линией. 

У людей аналогичная ситуация. Ни в одном исследовании не показано, что какое-то воздействие продлевает жизнь за счет замедления скорости старения человека. Например, Шпигельхальтер и Бреннер использовали закон Гомпертца. Они показали, что если в 2.2 или 2.7 раза (HR = 2,2 или 2.7) повысить смертность людей (А), которая не зависит от старения (G), то это равно потерянным 8 - 10 годам жизни при условии неизменности скорости старения. Именно столько курильщики и теряют.

При этом происходит параллельный сдвиг кривых выживания, а не изменение их наклона - как и у мышей в предыдущем исследовании. Эти наблюдения были справедливы для неоптимального потребления мяса, времени просмотра телевизора в сутки, ожирения, гиподинамии, потребления овощей и фруктов, терапии статинами [pubmed.ncbi.nlm.nih.gov/34151374] [pubmed.ncbi.nlm.nih.gov/27496144].

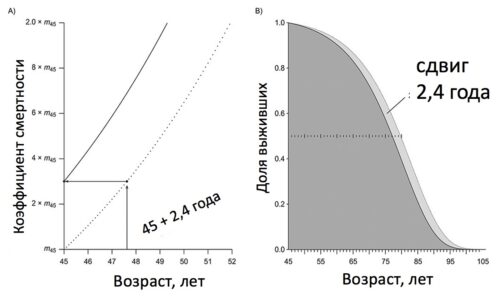
На рисунке показана взаимосвязь между возрастным параллельным сдвигом (на 2.4 года) кривых смертности (рисунок а) или кривых выживания (рисунок в) и разницей в ожидаемой продолжительности оставшейся жизни в гипотетическом примере [pubmed.ncbi.nlm.nih.gov/34151374].

Удивительно, что какой бы метод продления жизни для людей не применялся, постоянно наблюдается достаточно параллельный сдвиг кривых выживания. И нужно только посчитать размер этого сдвига в годах [pubmed.ncbi.nlm.nih.gov/34151374].

Плохая новость, что нам пока не удается замедлить скорость старения людей. Хорошая новость заключается в том, что мы можем продлевать жизнь без уменьшения скорости старения за счет снижения риска смертности (А), которая не зависит от скорости старения (G) по Гомпертцу R(t) = A*e^(G*t).

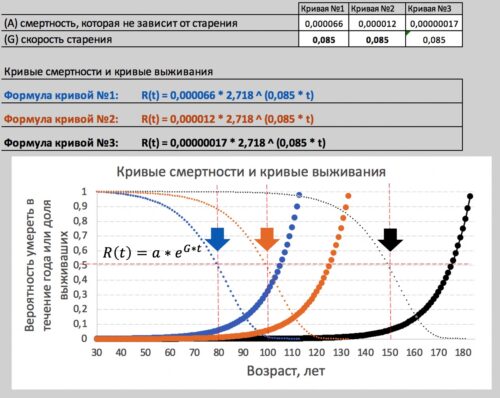
Рисунок. Чтобы увеличить ожидаемую продолжительность жизни до 150 лет, нужно снизить не зависящую от старения смертность (А) в 388 раз (c 0.000066 до 0.00000017), что невозможно - черная кривая в сравнении с синей.Тогда как снизить смертность в 5.5 раз (с 0.000066 до 0.000012) и продлить ожидаемую продолжительность жизни на 20 лет (с 80 до 100 лет) можно с помощью здорового образа жизни в совокупности с хорошим медицинским обследованием - оранжевая кривая в сравнении с синей.

Многие ученые, изучающие старение, даже не заботились о своем здоровье – не снижали свою уязвимость к болезням (А) при неизменной скорости старения (G). Некоторые из них ушли слишком рано. Так Вайсерман Александр Михайлович (докт. мед. наук, зав. лабораторией эпигенетики ГУ “Институт геронтологии им. Д.Ф. Чеботарева” НАМН Украины, Киев, Украина) ушел из жизни всего в 64 года. 

20 лет на дороге не валяются. Поэтому бросаем курить, покупаем кроссовки, учимся правильно питаться, что снизит риск смертности в 3,84 раза [ncbi.nlm.nih.gov/pubmed/29712712]. А также вовремя делаем анализы крови и УЗИ сосудов шеи, чтобы в сумме со здоровым образом жизни снизить смертность в 5 раз и продлить жизнь примерно на 20 лет.

И это не продление жизни на 20 лет в "дряхлом теле", как многие думают, а продление здоровой, трудоспособной продолжительности жизни. Дело в том, что чем выше продолжительность жизни, тем выше здоровая, трудоспособная продолжительность жизни. 

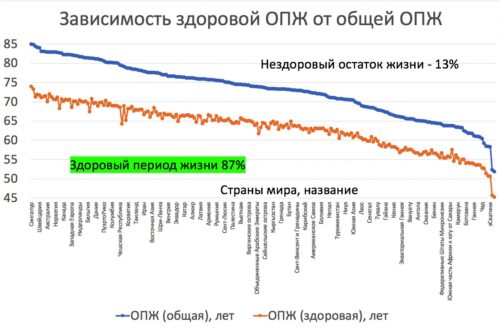
Рисунок. Зависимость здоровой ожидаемой продолжительности жизни (ОПЖ) от общей продолжительности жизни во всех странах мира в 2019 году - генеральная совокупность всех людей на планете. Исследование опубликовано в журнале Ланцет [thelancet.com/journals/lancet/article/PIIS0140-6736(20)30977-6/fulltext]. Здоровая продолжительность жизни без инвалидности составляет в среднем 87% от общей продолжительности жизни. 

А теперь давайте выберем способ оценки, который будем использовать для создания часов долголетия. Это может быть любой расчетный риск, который применяется в исследованиях. Например, отношение опасности (Hazard Ratio) или HR. В мире очень много различных исследований, в которых проверяется, как лекарства сокращают или увеличивают риск смертности в течение 10 лет. Hazard Ratio и другие метрики используют для оценки такого риска. Но у читателя возникает логичный вопрос. Как за 10 лет можно узнать, на сколько лет продлит жизнь тот или иной способ? Разве для этого же нужно ждать всю жизнь? Мы ответим на этот вопрос позже. А пока давайте рассмотрим, как определяют Hazard Ratio. 

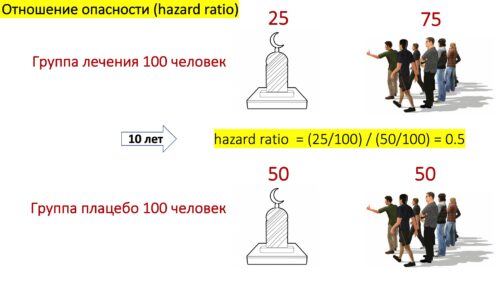На рисунке показан расчет Hazard Ratio. Есть две группы людей по 100 человек в каждой. Одна группа пьет лекарство. Через 10 лет в ней умирает 25 человек, а 75 еще живы. Вторая группа никак не лечится. Через 10 лет во второй группе умирают 50 человек. Теперь посчитаем Hazard Ratio = (25/100) / (50/100) = 0.5. То есть Hazard Ratio для первой группы = 0.5, а во второй группе 1. Так как 0.5 в 2 раза меньше, чем 1, то делаем вывод, что лечение лекарством сократило риск смертности в течение 10 лет в 2 раза. 

Если Hazard Ratio (HR) сокращается в 2 раза, значит смертность (А), которая не зависит от скорости старения, также сокращается в 2 раза при неизменной скорости, с которой растет риск (G), согласно закону Гомпертца. Вспоминаем, что закон Гомпертца выглядит так R(t) = A*e^(G*t):

• R(t) = A*e^(G*t) - уравнение Гомпертца для группы, которая не лечилась
• R(t) = (1/2 * A)*e^(G*t) - уравнение Гомпертца для группы, которую лечили лекарством
• HR=(0.5∗ А)/a=0.5
• Если А сокращается в два раза, то и Hazard Ratio сокращается в 2 раза

Таким образом, если в исследовании Hazard Ratio сокращается в 2 раза, мы можем во столько же раз сократить и (А) в уравнении Гомпертца, при условии неизменной скорости старения (G). Почему мы делаем такое допущение о неизменной скорости старения (G)? Как мы уже рассмотрели выше, ученым до сих пор еще никаким способом не удалось продлить жизнь людям замедлением скорости старения (G). Поэтому до тех пор, пока мы не придумаем, как продлить жизнь и одновременно замедлить скорость старения человека (G), мы можем опираться на это допущение.

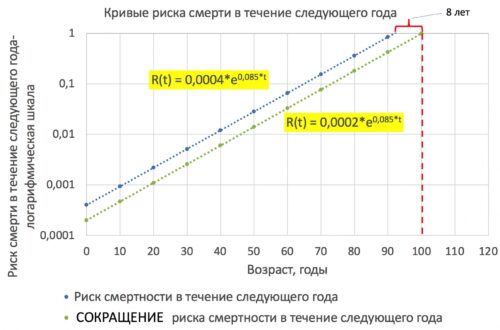А раз продление жизни людей, как и мышей и других млекопитающих сопровождается только параллельным сдвигом кривых смертности или кривых выживаемости, ведь скорость старения (G) не меняется, то мы можем использовать этот параллельный сдвиг и для прогноза продления или сокращения жизни даже, если исследование проводилось всего 5-10 лет. И действительно, достаточно понять, что за 5-10 лет смертность снизилась в 2 раза, как можно это использовать для нового уравнения Гомпертца R(t) = (1/2 * A)*e^(G*t), где 1/2 - это сокращение смертности в 2 раза. И в результате рассчитать сколько вообще проживет человек в сумме.

Рисунок демонстрирует такой расчет графически. Синяя кривая смертности имеет уравнение R(t) = 0.0004*e^(0.085*t), а зеленая кривая смертности имеет уравнение R(t) = (1/2 * 0.0004)*e^(0.085*t), так как смертность сократилась в 2 раза (1/2), что эквивалентно продлению жизни на 8 лет. 

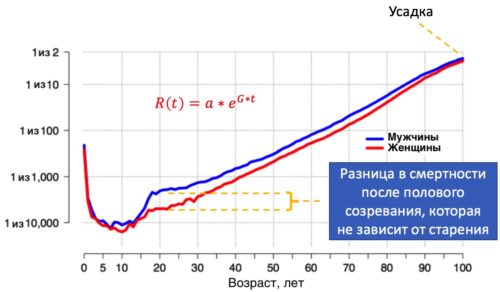Что еще нам нужно учесть для прогноза продолжительности жизни? Дело в том, что в реальности, хотя кривые смертности, например, для мужчин и женщин достаточно параллельны друг другу, но к поздним возрастам они встречаются друг с другом - имеют "усадку".

На рисунке ежегодный риск смерти от всех причин для Англии и Уэльса, 2010-2012 гг. [pubmed.ncbi.nlm.nih.gov/27496144]. Кривые смертности мужчин и женщин резко расходятся после полового созревания и затем на протяжении всей жизни достаточно параллельны, за исключением "усадки". 

Такая "усадка" - это не исключительное явление.

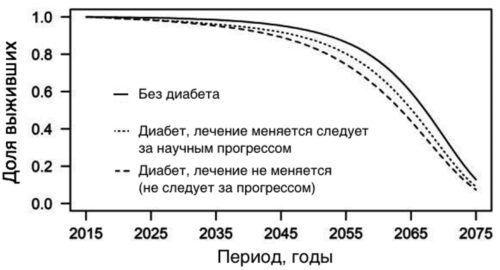
Она наблюдается каждый раз, когда мы оцениваем кривые смертности или кривые выживания. Аналогичная ситуация и по сахарному диабету 2-го типа.

На рисунке показано, что хотя сахарный диабет и сокращает ожидаемую продолжительность жизни людей, и кривые выживания больных и здоровых достаточно параллельны относительно друг друга, но они имеют "усадку" к концу продолжительности жизни наблюдаемых групп людей. 

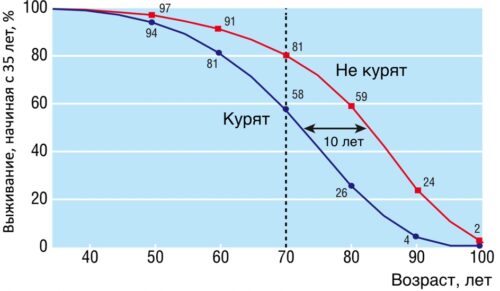Хотя курение сокращает жизнь, но оно не ускоряет старение людей.

Кривые выживания людей, которые курят, и тех, кто не курят, достаточно параллельны с "усадкой" к концу жизни, как показано на рисунке [pubmed.ncbi.nlm.nih.gov/15213107].

Учитывая эти закономерности, Александр Фединцев примерно в 2018 году предложил формулу, которая превращает риски в годы жизни [docs.google.com/document/d/1YV1tmEZmjpZzAVqxek8Gj4LmKDMBIZecjCqjDZpmZxE/edit?usp=drivesdk].

А в 2021 году была опубликована еще одна статья с подобной логикой расчета и с учетом "усадки" [pubmed.ncbi.nlm.nih.gov/34151374]. 

На рисунке показано, как превратить Hazard Ratio (HR) в годы жизни. Допустим, мы нашли какое-то исследование и прочитали в нем, что терапия каким-то лекарством в течение 10 лет сократила смертность в 2 раза (HR = 0.5). И вот теперь для человека в возрасте 40 лет нам нужно узнать, сколько лет жизни добавит лечение таким лекарством, если оно ему показано. Наши исходные данные: HR = 0.5 и возраст 40 лет. Подставляем эти данные в формулу, которая показана на картинке, и получаем, что лечение таким лекарством добавит 40-летнему человеку 6.6 лет жизни. Это конечно не гарантия, а среднее вероятных исходов.

Но все эти расчеты сложные. Чтобы было проще, можно просто скачать калькулятор, который работает в программе Microsoft Excel.

Скачайте калькулятор перевода риска HR в годы жизни по ссылке nestarenie.ru/kal_HR.xlsx, введите свой возраст, введите риск HR, введите доверительные интервалы, и вы получите оценку добавленных или потерянных лет жизни.

В исследовании вы можете встретить такую запись значения риска HR, как например, HR: 0.5, 95% CI: 0.35, 0.65. Где HR = 0.35 и 0.65 - это нижняя и верхняя границы доверительного интервала. 

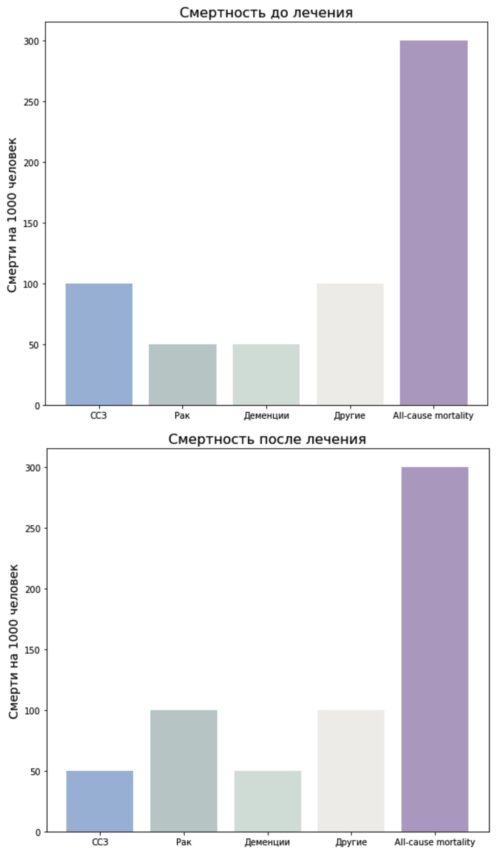
Также важно, что для прогноза годится только HR, которое описывает не риск смерти от отдельных причин, а риск от всех причин (all-cause mortality). 

All-cause mortality защищает от манипуляций с причинами смертности. Действительно ли полезно избежать смерти от сердечного приступа, если лечение просто означает, что вместо этого вы умрете от рака?

На сегодня очень многие исследования, которые проверяют в клинических исследованиях эффективность лекарств, диет и так далее, оценивают риск смертности на дистанции 5-10 и более лет, применяя Hazard Ratio для смертности от всех причин (all-cause mortality). Зная Hazard Ratio, используя методику, которая рассмотрена в этой статье, мы легко можем узнать, на сколько лет продлевает жизнь терапия, диета и так далее. 

Итак, мы с вами создали часы долголетия. Если Вам понравилась эта статья, и есть желание помочь развитию проекта, то помощь приветствуется - по ссылке.