Математика нестарения. Часть -5. Ставить эксперименты на людях по продлению жизни не долго – достаточно подождать 5-10 лет

Мало вероятно, что отдельные методы и комбинации методов, увеличивавших продолжительность жизни в экспериментах на мышах, смогут увеличить максимальную продолжительность жизни (МПЖ) человека. Вспомним мышей с синдромом Ларона. Мыши «Ларона» с нокаутом генов, кодирующих рецепторы гормона роста [pubmed.ncbi.nlm.nih.gov/15536017] живут до 1560 дней – почти как при сокращении калорийности питания. Это рекордно много. Однако, продолжительность жизни людей с синдромом Ларона не больше, чем у их родственников без синдрома Ларона [ncbi.nlm.nih.gov/pubmed/21325617]. Кто еще сомневается, читайте статью "Методы, продлевавшие жизнь мышам, бесполезны для человека".

Пора переходить от исследований биологии старения мышей к исследованиям биологии старения человека. Люди потому и живут долго, что большинство известных проблем, ограничивающих жизнь коротко живущих животных, биология человека уже решила.

Но как только заходит речь об экспериментах на людях, сразу многим логично кажется, что такие эксперименты ждать слишком долго. Человек ведь живет до 100 лет. В этой статье мы увидим, что это не так. Достаточно подождать 5-10 лет. Как это работает?

1. Доказательная медицина уже сегодня содержит много экспериментов, в которых лекарства или иные методы, продлевали жизнь людям. Как узнать, читая научное исследование, на сколько лет увеличивает продолжительность жизни то или иное лекарство? Подробнее, как это рассчитать, можно прочитать в статье "Как узнать, на сколько лет продлевает жизнь то или иное лекарство". В данной статье мы не рассматриваем, как это посчитать, но разберемся, почему это посчитать в принципе возможно. Из этических соображений рассмотрим далее пример не на людях, а на животных.

2. Допустим мы решили поставить эксперимент на мухах дрозофилах, в результате которого определили, что исследуемое нами лекарство в течение 1-ой недели сократило вероятность умереть в 2 раза. Затем мы увидели такой же результат и в следующие 2-3 недели. Можно лишь на основании нескольких недель исследования сделать прогноз увеличения продолжительности жизни, не наблюдая за мухами до самой их смерти при условии, что скорость старения мух не менялась?

3. Да. Это возможно. Для этого необходимо воспользоваться уравнением Гомпертца. Закон смертности Гомпертца - R(t) = A * e ^ (G*t). Впервые закон смертности Гомпертца был опубликован актуарием и математиком Бенджамином Гомпертцем в 1825 году [royalsocietypublishing.org/doi/10.1098/rstl.1825.0026]. Согласно этому закону, риск умереть с возрастом растет по экспоненте со скоростью G. Скорость G - это скорость старения, на которую до сих пор не удавалось повлиять в экспериментах с млекопитающими [academic.oup.com/genetics/article/208/4/1617/6084259], а также [genetics.org/content/204/3/905]. Это плохая новость.

4. Но хорошая новость заключается в том, что закон Гомпертца R(t) = A * e ^ (G*t) хорошо предсказывает смертность животных. Также хорошая новость заключается в том, что при неизменной скорости старения G достаточно уменьшить только лишь базовый уровень смертности, который в уравнении Гомпертца обозначается буквой A, чтобы увеличить продолжительность жизни животных. Давайте для начала рассмотрим пример на животных.

5. Итак. Допустим исследование показало снижение общей смертности мух дрозофилов в 2 раза. Допустим скорость старения дрозофилов G = 0.4847. Допустим базовый риск общей смертности дрозофилов был 0.01, а стал 0.005. Тогда уравнение Гомпертца изначально имеющее вид: R(t) = 0.01 * e ^ (0.4847*t), изменится так: R(t) = 0.005 * e ^ (0.4847*t). 

Рисунки 1 и 2. Логарифмическая шкала, отражающая увеличение продолжительности жизни мух дрозофилов в результате снижения базовой смертности в 2 раза - с 0.01 до 0005.

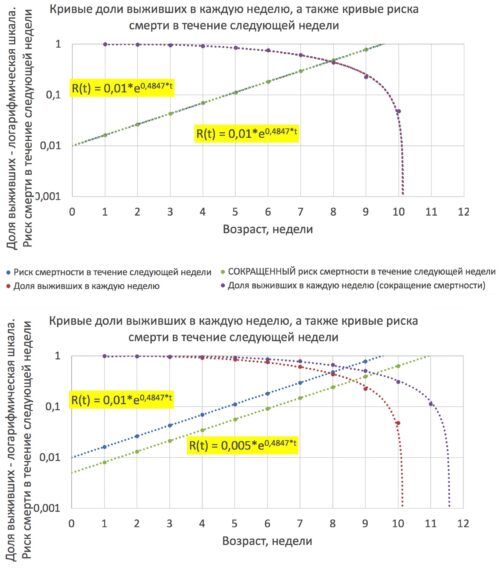
На рисунке 1 видно, что кривая смертности R(t) = 0.01 * e ^ (0.4847*t), берет начало в точке 0.01 по оси Y.  Это и означает, что базовый риск общей смертности дрозофилов был 0.01.

На рисунке 2 видно, что кривая смертности R(t) = 0.005 * e ^ (0.4847*t) берет начало в точке 0.005 по оси Y.  Это и означает, что базовый риск общей смертности дрозофилов снизился до 0.005.

В результате, как показано на рисунке 2, синяя кривая смертности R(t) = 0.01 * e ^ (0.4847*t) достигает вероятности смерти 1 (100%) по оси Y в возрасте 9.5 недель. Это означает, что мухи из группы, обозначенной синей линией, с вероятностью 100% умрут в период с 9.5 до 10.5 недель. Красная кривая выживания на рисунке 2 также показывает, что доля оставшихся в живых животных в возрасте 10 недель равна 0.

В результате, как показано на рисунке 2, зеленая кривая смертности R(t) = 0.005 * e ^ (0.4847*t) достигает вероятности смерти 1 (100%) по оси Y в возрасте 11 недель. Это означает, что мухи из группы, обозначенной синей линией, с вероятностью 100% умрут в период с 11 до 12 недель. Фиолетовая кривая выживания на рисунке 2 также показывает, что доля оставшихся в живых животных в возрасте 11.5 недель равна 0.

Таким образом, зная процент изменения риска смертности на каком-то отрезке жизни, можно предсказать добавленное или потерянное количество лет жизни. Примечание: такая модель работает при условии, что скорость старения не меняется. Но как мы рассмотрели выше, до сих пор еще ни в одном эксперименте не удавалось изменить скорость старения млекопитающих. А значит, наиболее вероятно, что любое лечение в эксперименте на людях изменяет лишь базовый риск смертности, а рассмотренная выше модель на основании лишь 5-10 лет эксперимента может предсказывать ожидаемую продолжительность жизни человека и приобретенные, либо потерянные годы жизни.

Предлагаем Вам оформить почтовую подписку на самые новые и актуальные новости, которые появляются в науке, а также новости нашей научно-просветительской группы, чтобы ничего не упустить. Обязательно оставляйте свои комментарии под статьей, которую вычитаете. Это очень важно для нас.

Автор статьи — Веремеенко Дмитрий Евгеньевич, сфера профессиональной деятельности - data science в медицине, машинное обучение, нейронные сети, основатель исследовательского проекта, изучающего терапии, направленные на увеличение продолжительности жизни человека (nestarenie.ru/slb-expert_.html), сооснователь сервиса для продления жизни Nestarenie_pro ., основатель форума о продлении жизни Nestarenie Camp (nestarenie.ru/camp.html), со-автор книги "Бонусные годы" (nestarenie.ru/kniga-3.html)., создатель справочного блога о старении человека (nestarenie.ru), Тел. +7 925 9244328 Dmitriy-tae@yandex.ru

Группа nestarenieRU в Вконтакте https://vk.com/nestarenie_ru

YouTube-канал https://www.youtube.com/c/nestarenieRU

Обязательно оставляйте свои комментарии под статьей, которую вычитаете. Это очень важно для нас.